PageRank: Power Iteration Animations

Outline for today

• Raw (Q) (dangling node)
• Corrected (P) (dangling fixed)
• Teleporting (G) (())

This page animates the iteration (x_{n+1} = Qx_n) on the 6-node PageRank example from Day 5.

• Node fill: value of (x_n) at that node.
• Labels: node index and (x_n) (rounded).
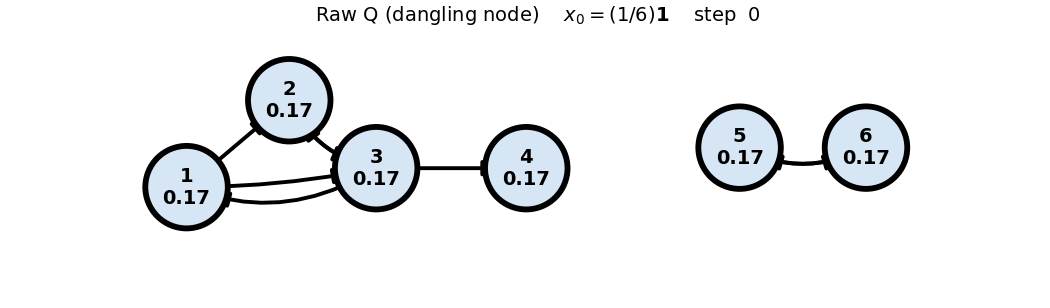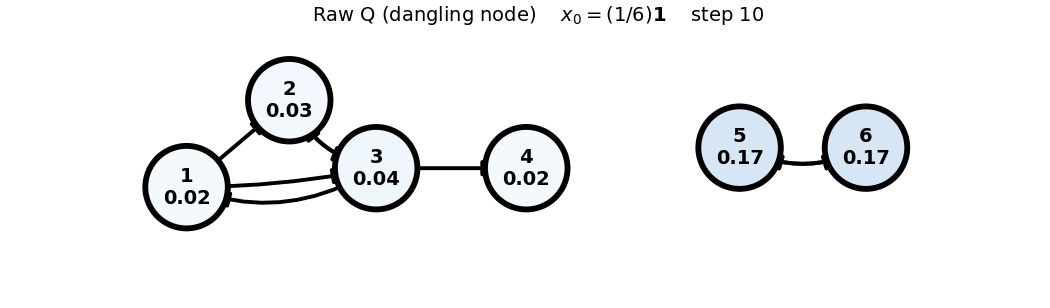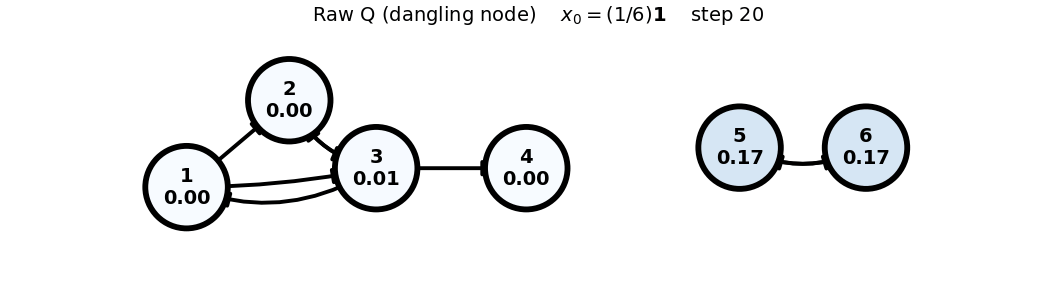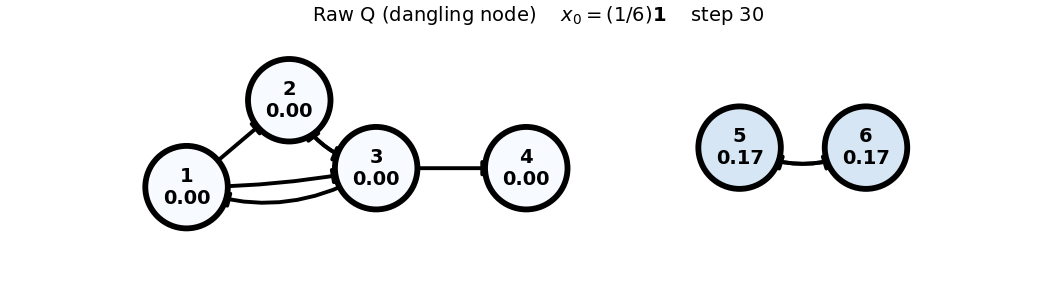
• Note: In the Raw (Q) case, the dangling node (4) causes loss of total mass; this is visible via sum(x) in the frame title.

Raw (Q) (dangling node)

x0: uniform

x_0 = (1/6)\mathbf{1}

Q = \begin{bmatrix} 0 & 0 & 1/3 & 0 & 0 & 0 \\ 1/2 & 0 & 1/3 & 0 & 0 & 0 \\ 1/2 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1/3 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 1 & 0 \end{bmatrix}, \quad x_0 = \begin{bmatrix} 1/6 \\ 1/6 \\ 1/6 \\ 1/6 \\ 1/6 \\ 1/6 \end{bmatrix}

x0: e1

x_0 = e_1

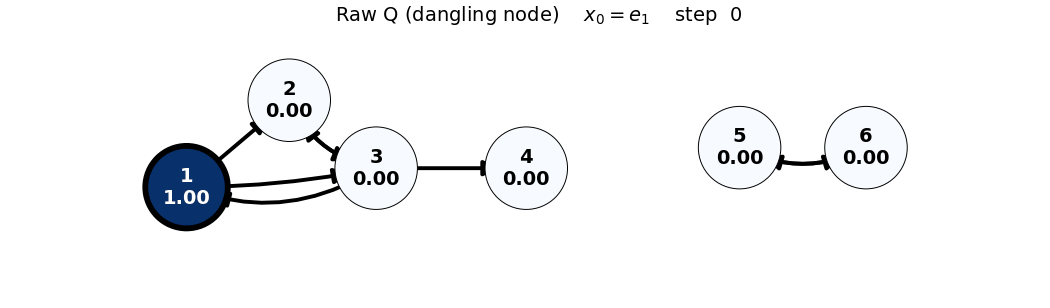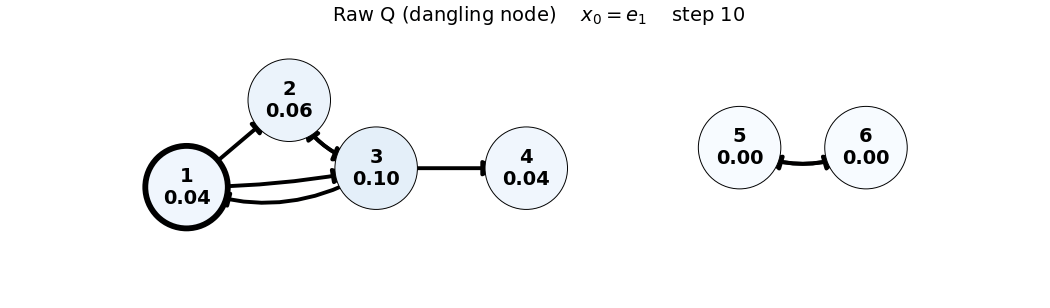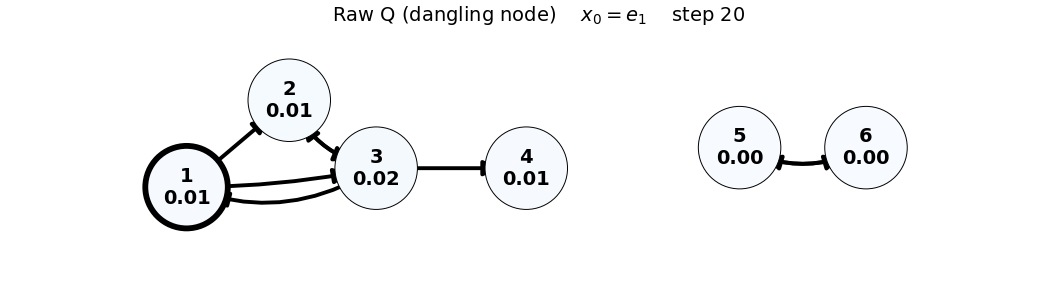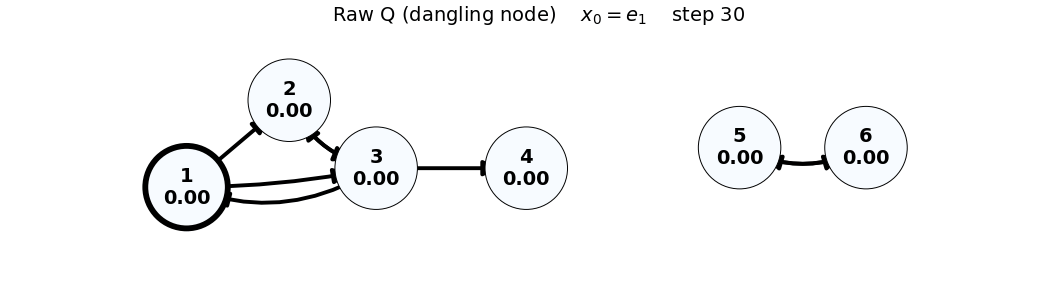
Q = \begin{bmatrix} 0 & 0 & 1/3 & 0 & 0 & 0 \\ 1/2 & 0 & 1/3 & 0 & 0 & 0 \\ 1/2 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1/3 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 1 & 0 \end{bmatrix}, \quad x_0 = \begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix}

x0: e4

x_0 = e_4

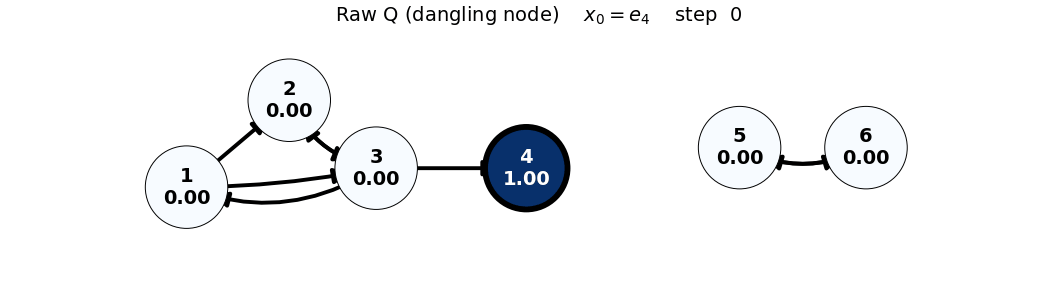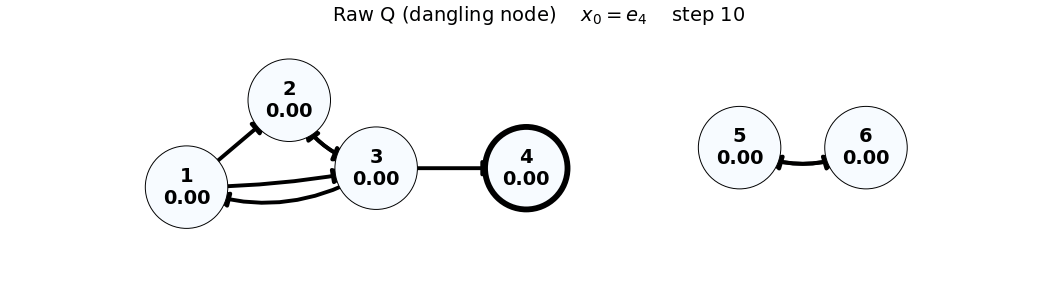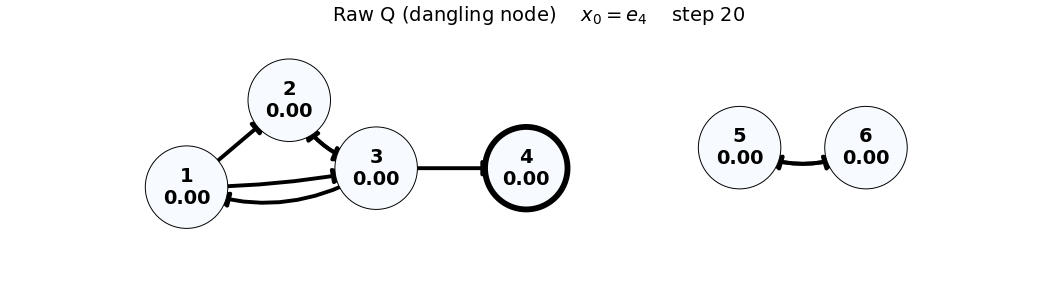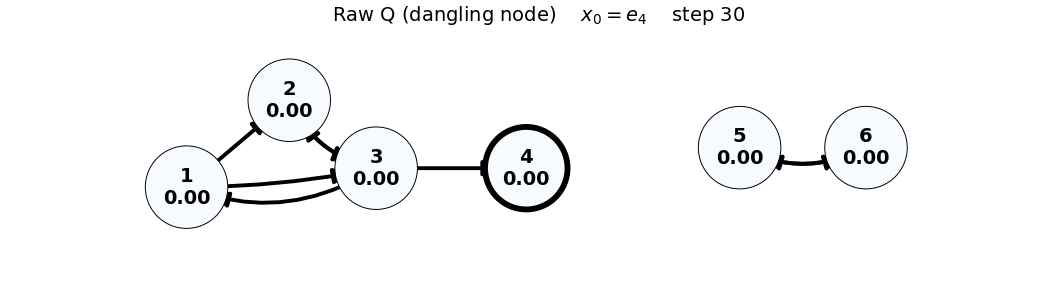
Q = \begin{bmatrix} 0 & 0 & 1/3 & 0 & 0 & 0 \\ 1/2 & 0 & 1/3 & 0 & 0 & 0 \\ 1/2 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1/3 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 1 & 0 \end{bmatrix}, \quad x_0 = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \\ 0 \\ 0 \end{bmatrix}

x0: e5

x_0 = e_5

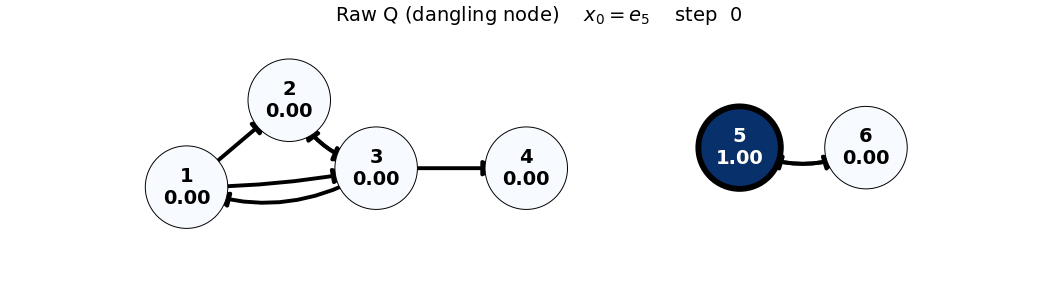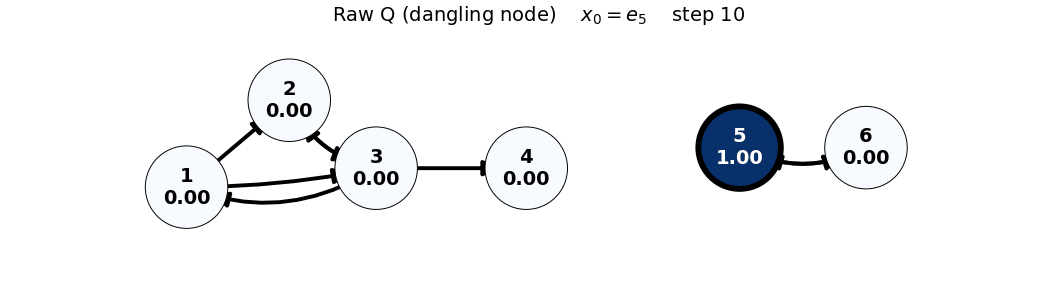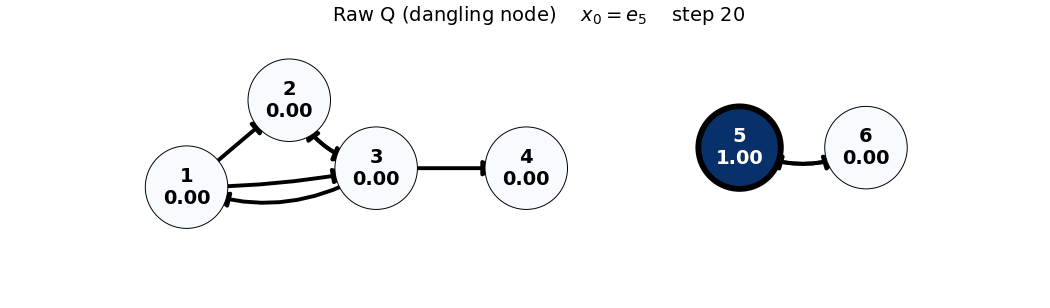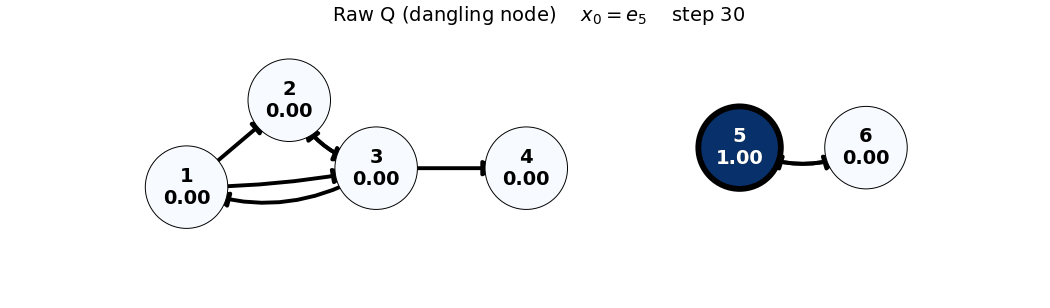
Q = \begin{bmatrix} 0 & 0 & 1/3 & 0 & 0 & 0 \\ 1/2 & 0 & 1/3 & 0 & 0 & 0 \\ 1/2 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1/3 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 1 & 0 \end{bmatrix}, \quad x_0 = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 1 \\ 0 \end{bmatrix}

Final States (Raw (Q))

Final states after 30 iterations for each starting vector:

Uniform: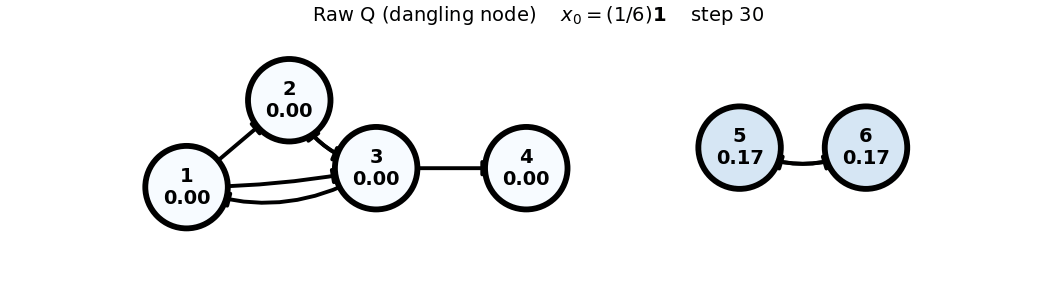

e_1: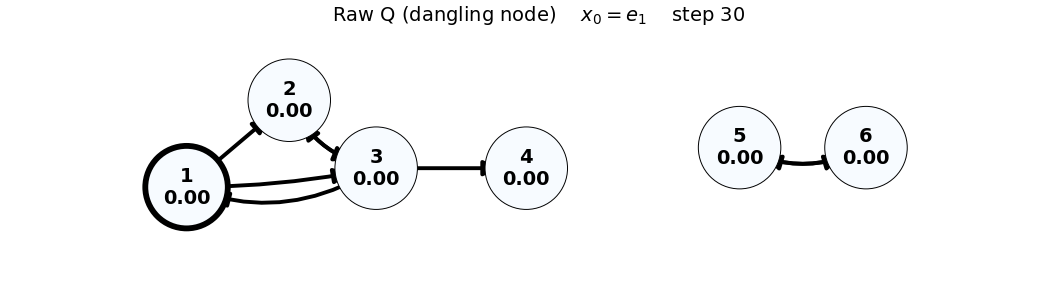

e_4: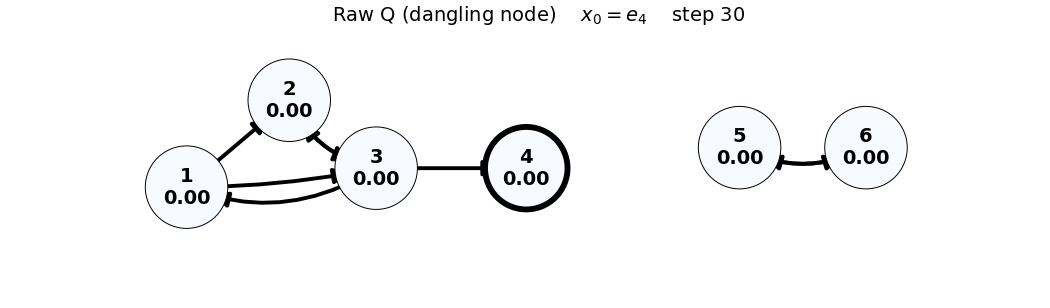

e_5: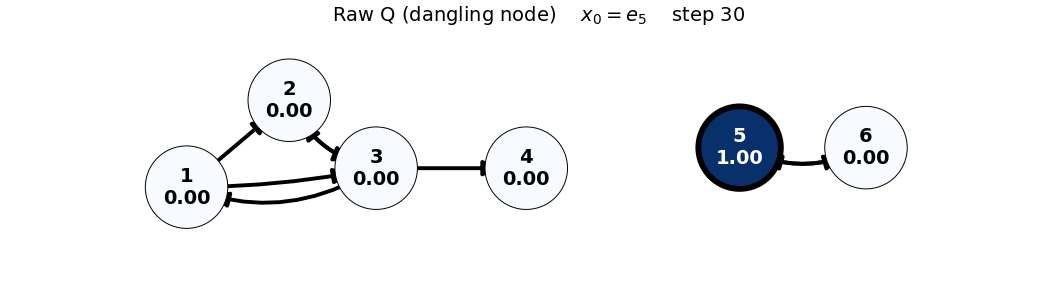

Corrected (P) (dangling fixed)

x0: uniform

x_0 = (1/6)\mathbf{1}

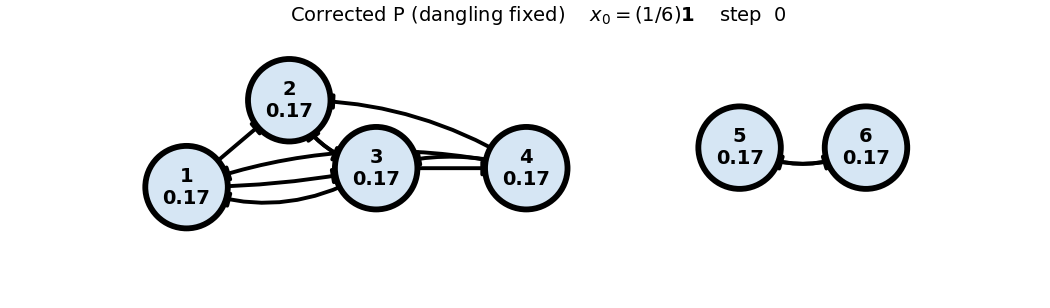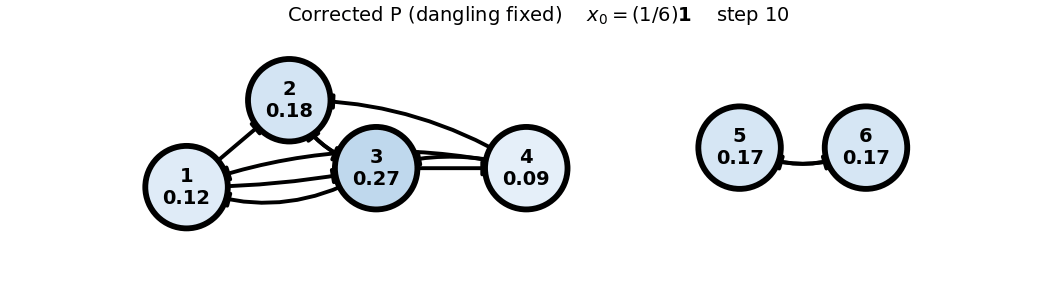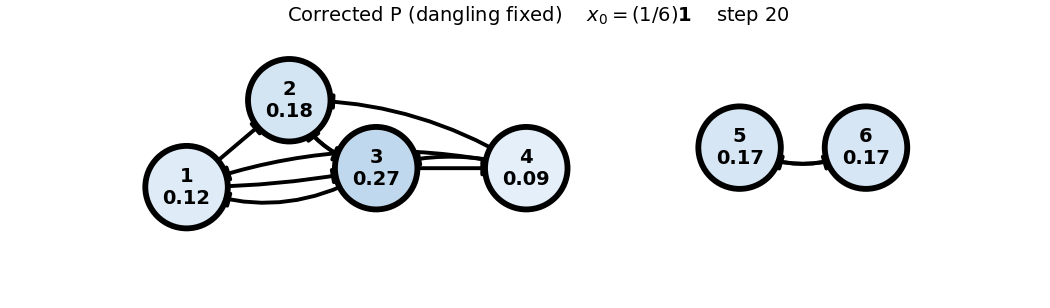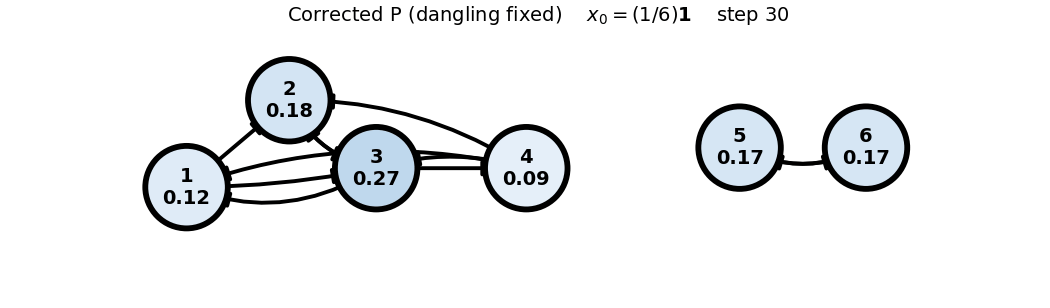
P = \begin{bmatrix} 0 & 0 & 1/3 & 1/3 & 0 & 0 \\ 1/2 & 0 & 1/3 & 1/3 & 0 & 0 \\ 1/2 & 1 & 0 & 1/3 & 0 & 0 \\ 0 & 0 & 1/3 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 1 & 0 \end{bmatrix}, \quad x_0 = \begin{bmatrix} 1/6 \\ 1/6 \\ 1/6 \\ 1/6 \\ 1/6 \\ 1/6 \end{bmatrix}

x0: e1

x_0 = e_1

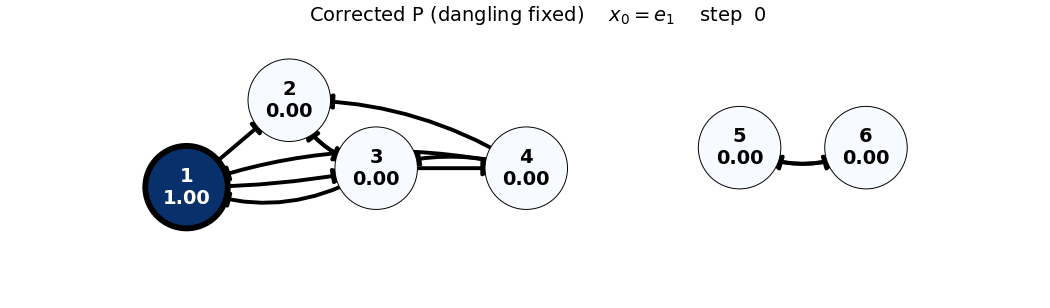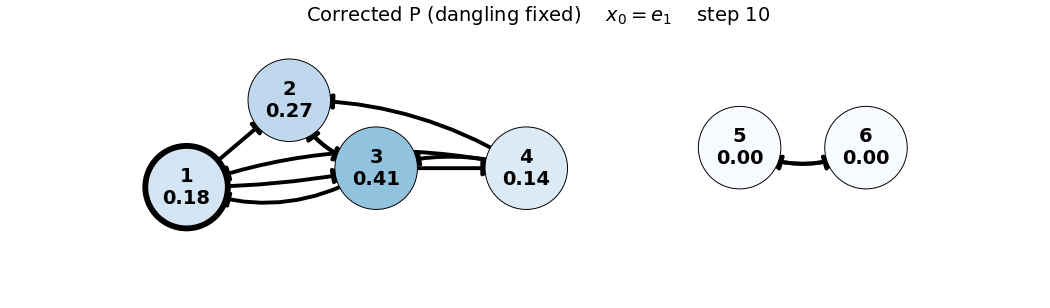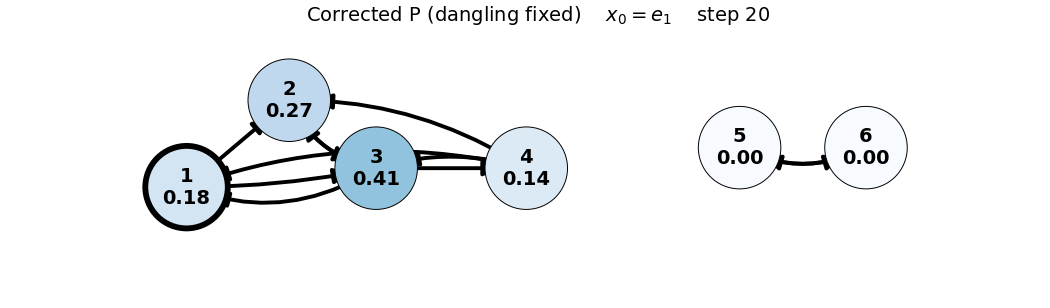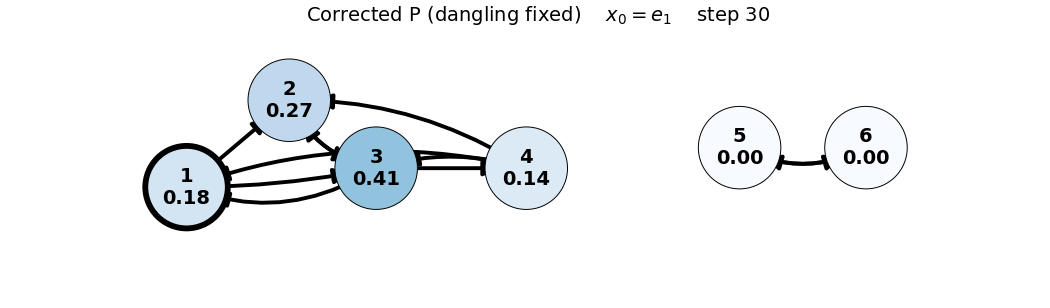
P = \begin{bmatrix} 0 & 0 & 1/3 & 1/3 & 0 & 0 \\ 1/2 & 0 & 1/3 & 1/3 & 0 & 0 \\ 1/2 & 1 & 0 & 1/3 & 0 & 0 \\ 0 & 0 & 1/3 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 1 & 0 \end{bmatrix}, \quad x_0 = \begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix}

x0: e4

x_0 = e_4

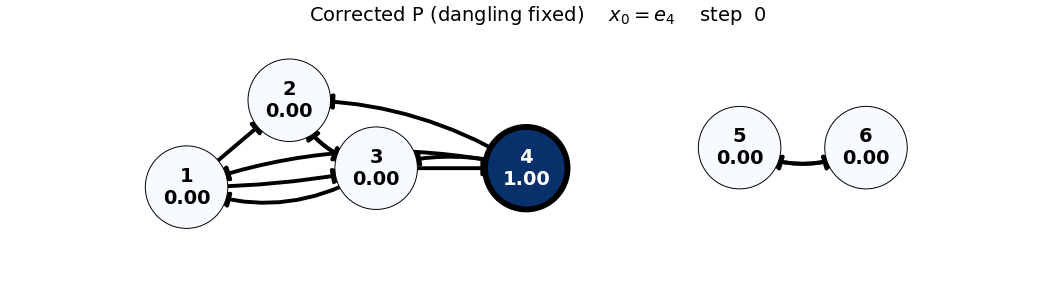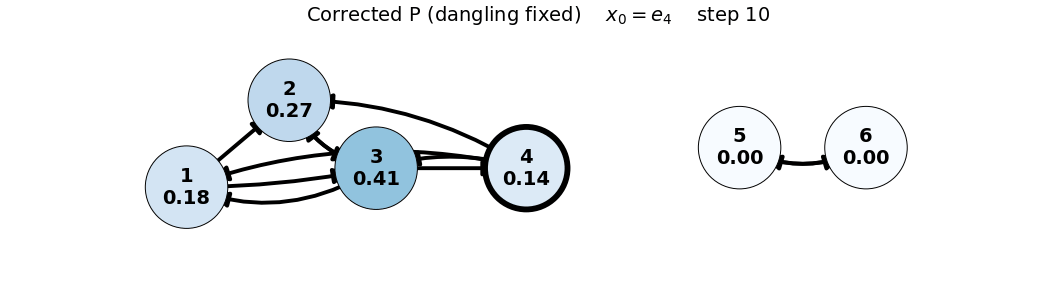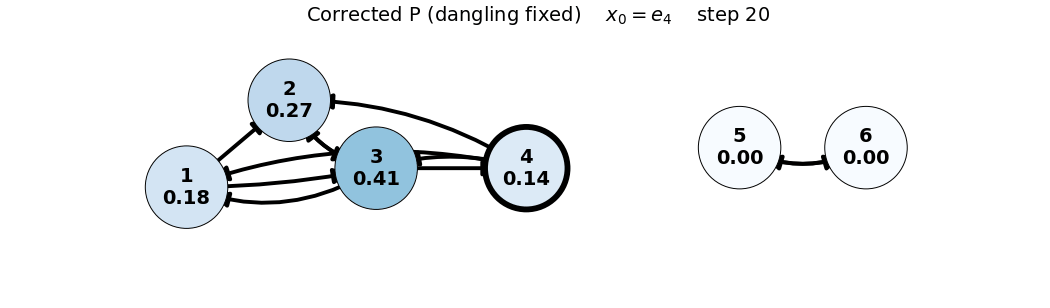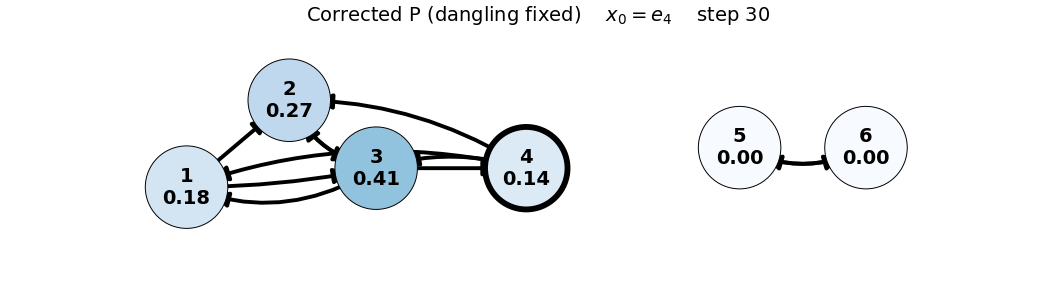
P = \begin{bmatrix} 0 & 0 & 1/3 & 1/3 & 0 & 0 \\ 1/2 & 0 & 1/3 & 1/3 & 0 & 0 \\ 1/2 & 1 & 0 & 1/3 & 0 & 0 \\ 0 & 0 & 1/3 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 1 & 0 \end{bmatrix}, \quad x_0 = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \\ 0 \\ 0 \end{bmatrix}

x0: e5

x_0 = e_5

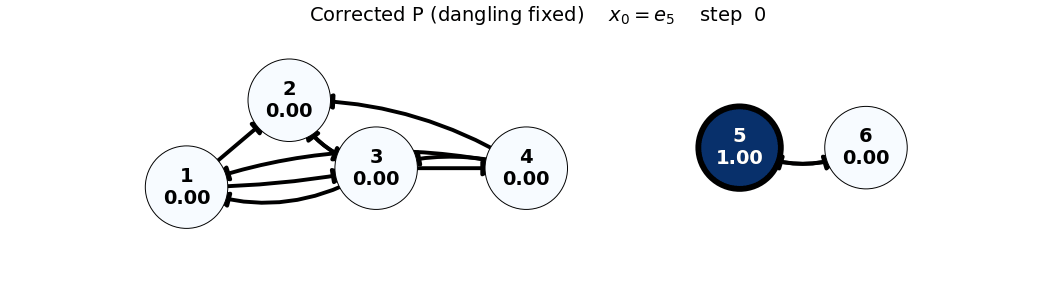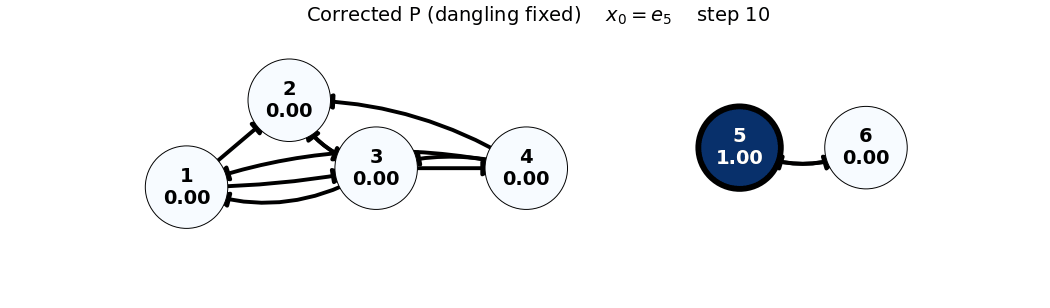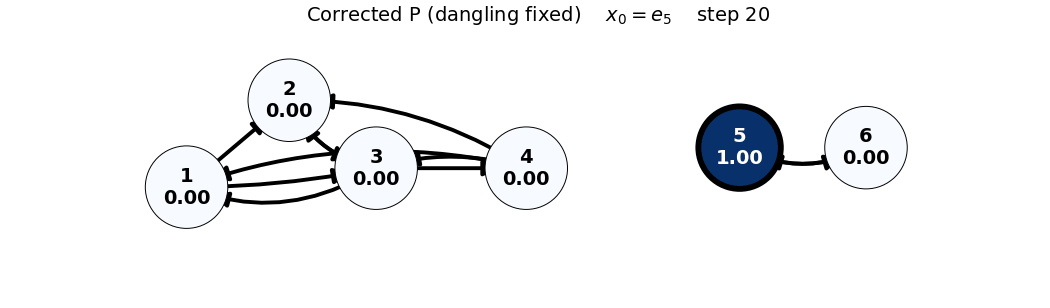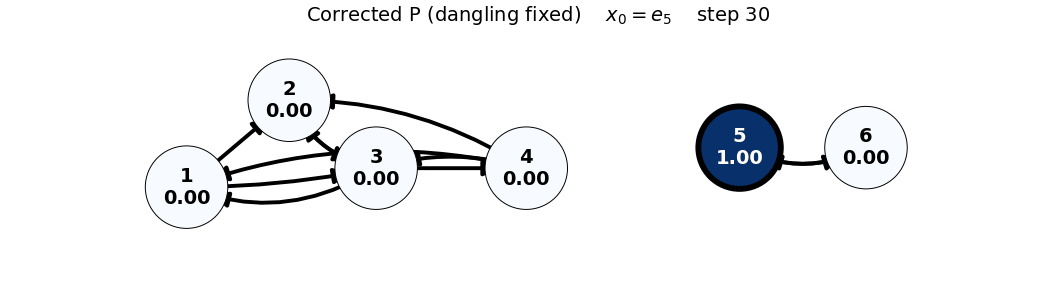
P = \begin{bmatrix} 0 & 0 & 1/3 & 1/3 & 0 & 0 \\ 1/2 & 0 & 1/3 & 1/3 & 0 & 0 \\ 1/2 & 1 & 0 & 1/3 & 0 & 0 \\ 0 & 0 & 1/3 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 1 & 0 \end{bmatrix}, \quad x_0 = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 1 \\ 0 \end{bmatrix}

Final States (Corrected (P))

Final states after 30 iterations for each starting vector:

Uniform: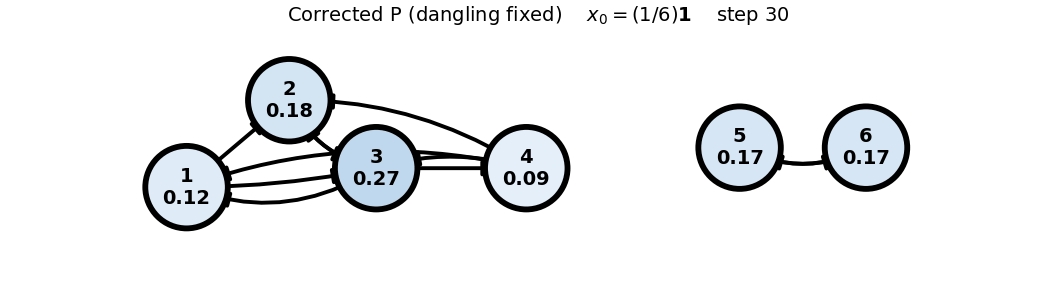

e_1: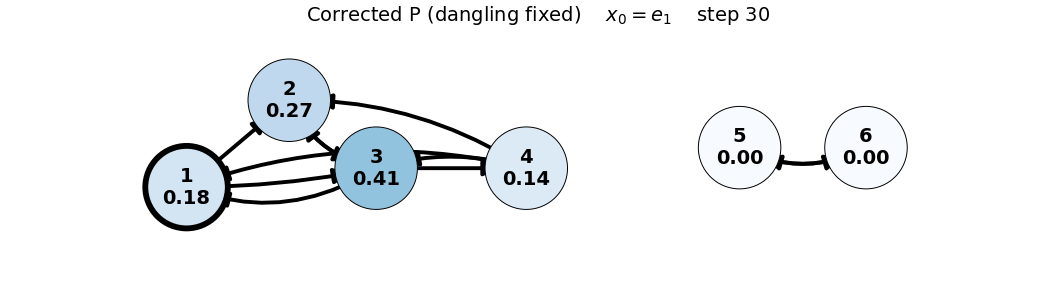

e_4: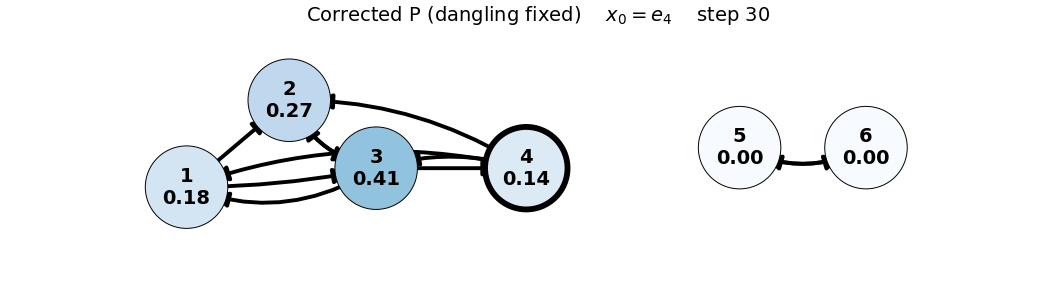

e_5: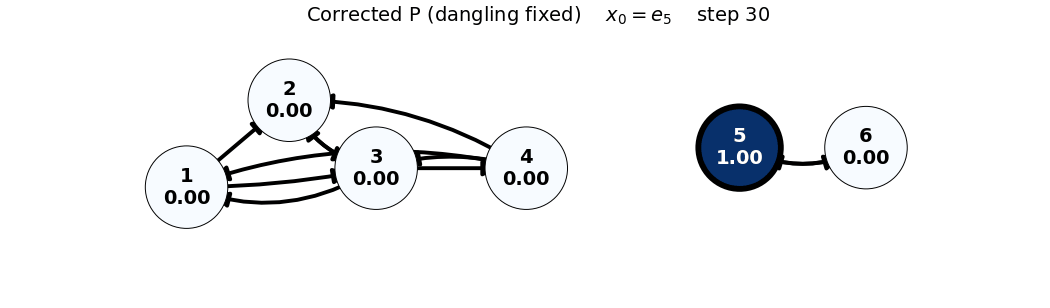

Teleporting (G) (())

x0: uniform

x_0 = (1/6)\mathbf{1}

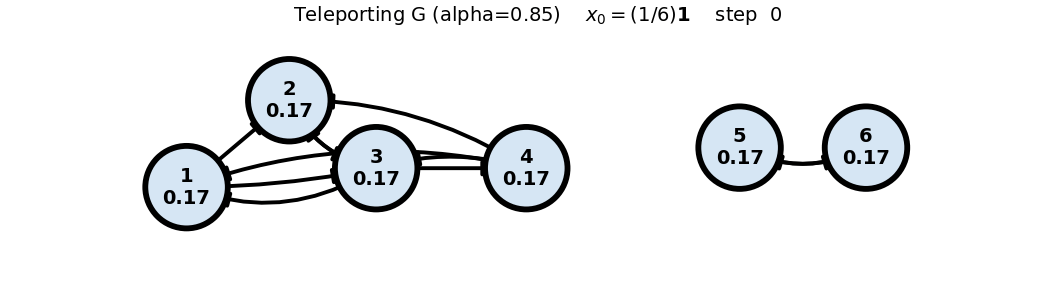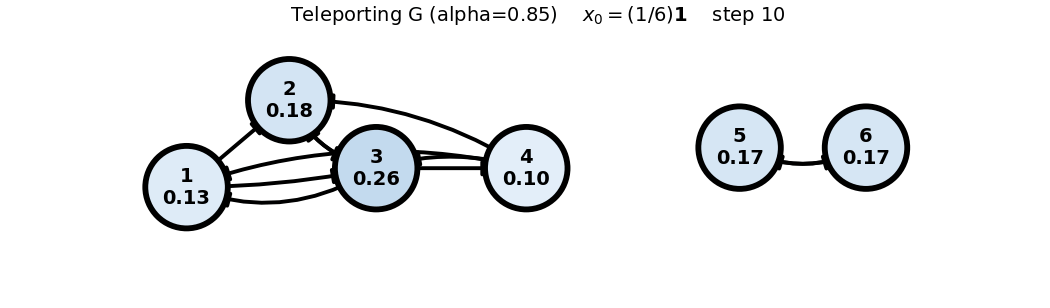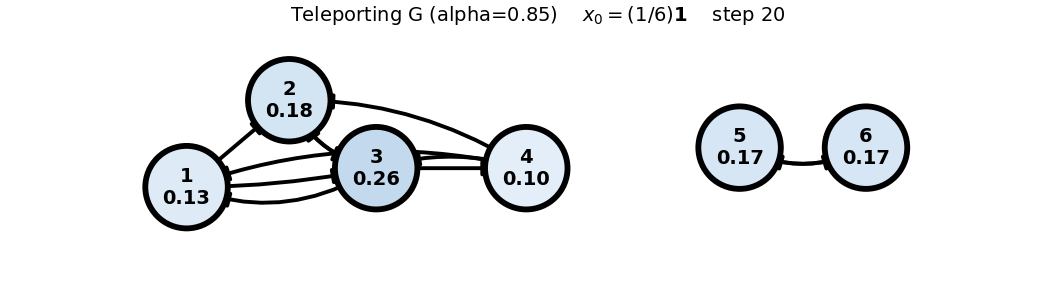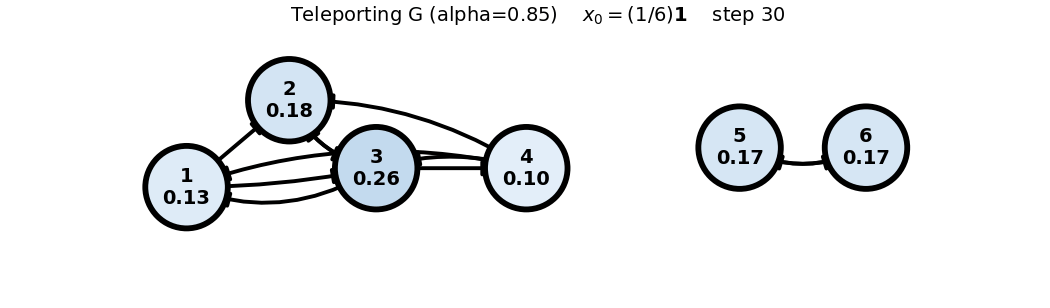
G = 0.85 P + 0.15 \frac{1}{6}\mathbf{1}\mathbf{1}^T = 0.85 P + 0.025 \begin{bmatrix} 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 \end{bmatrix}, \quad x_0 = \begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix}

x0: e1

x_0 = e_1

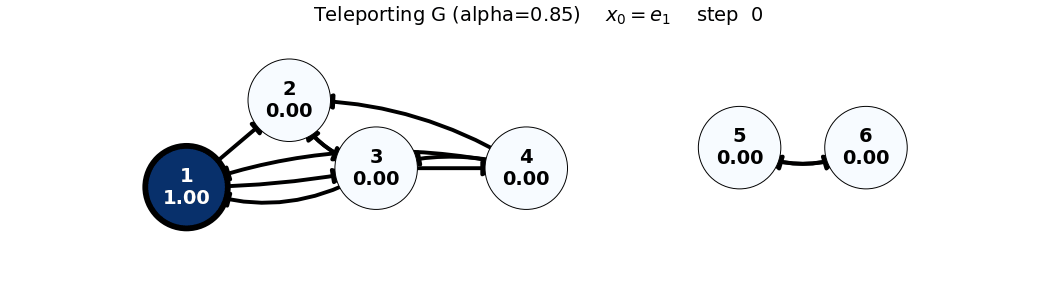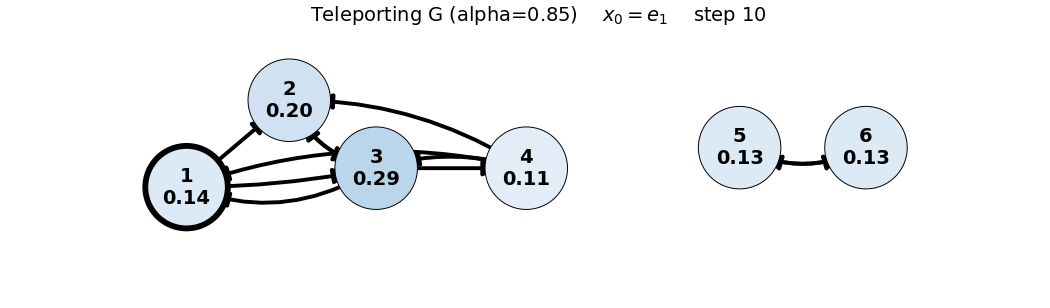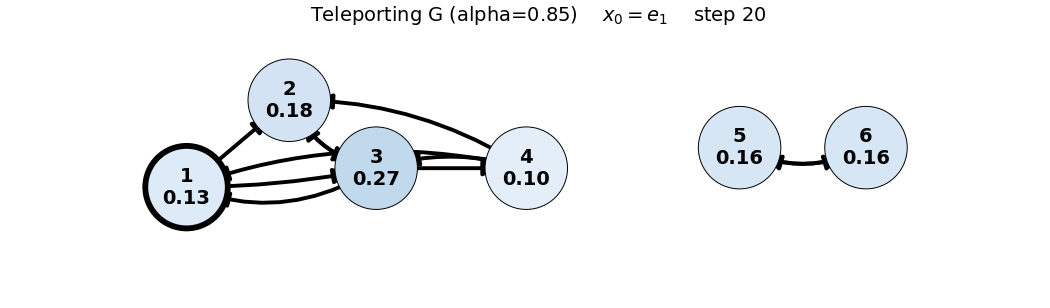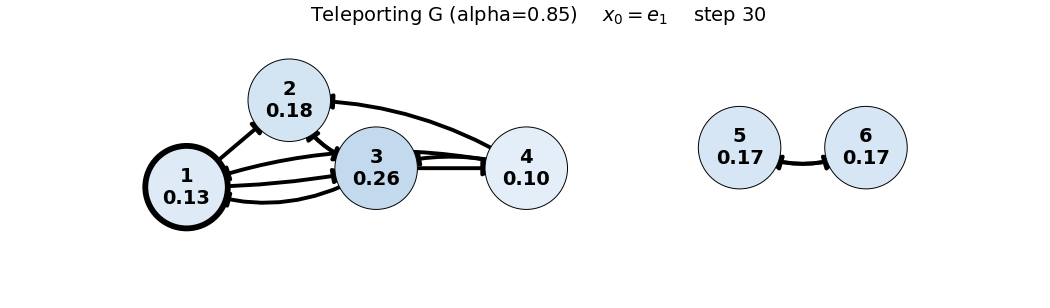
G = 0.85 P + 0.15 \frac{1}{6}\mathbf{1}\mathbf{1}^T = 0.85 P + 0.025 \begin{bmatrix} 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 \end{bmatrix}, \quad x_0 = \begin{bmatrix} 1/6 \\ 1/6 \\ 1/6 \\ 1/6 \\ 1/6 \\ 1/6 \end{bmatrix}

x0: e4

x_0 = e_4

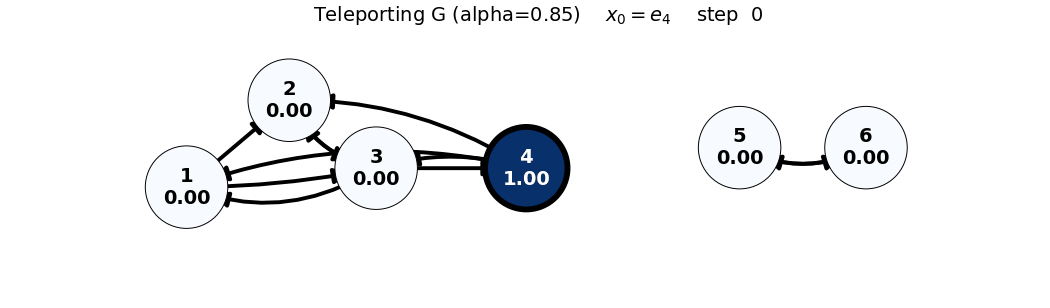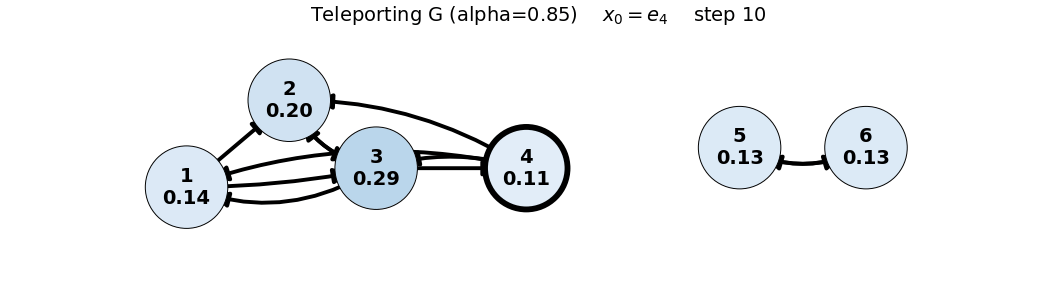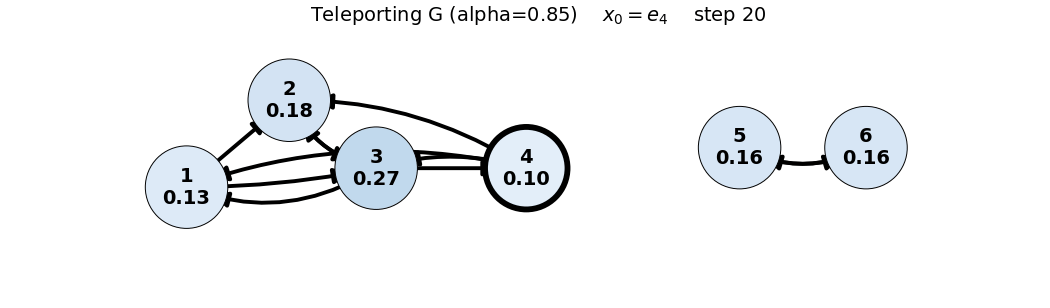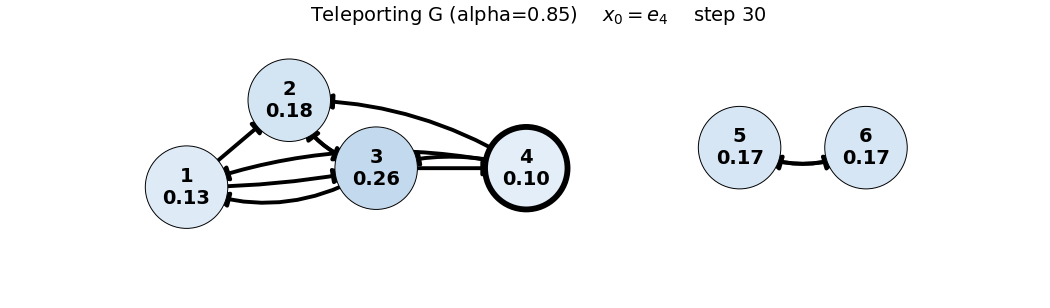
G = 0.85 P + 0.15 \frac{1}{6}\mathbf{1}\mathbf{1}^T = 0.85 P + 0.025 \begin{bmatrix} 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 \end{bmatrix}, \quad x_0 = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \\ 0 \\ 0 \end{bmatrix}

x0: e5

x_0 = e_5

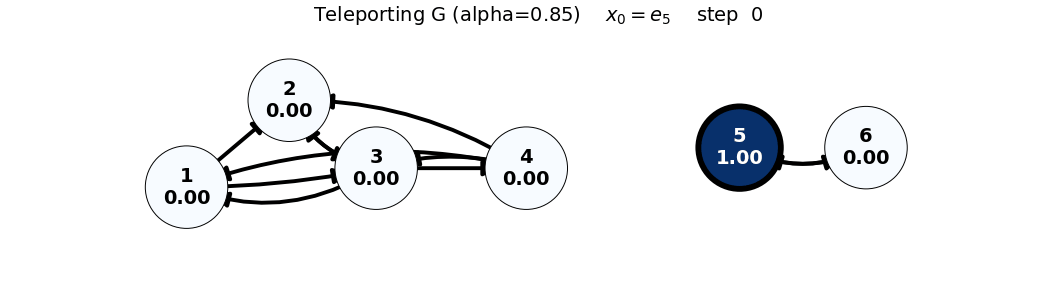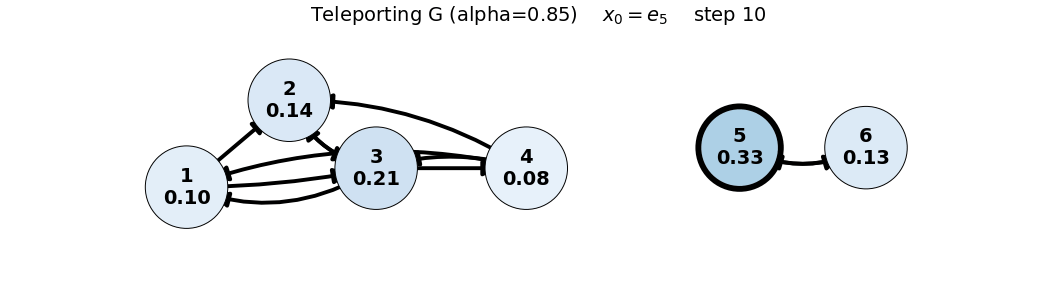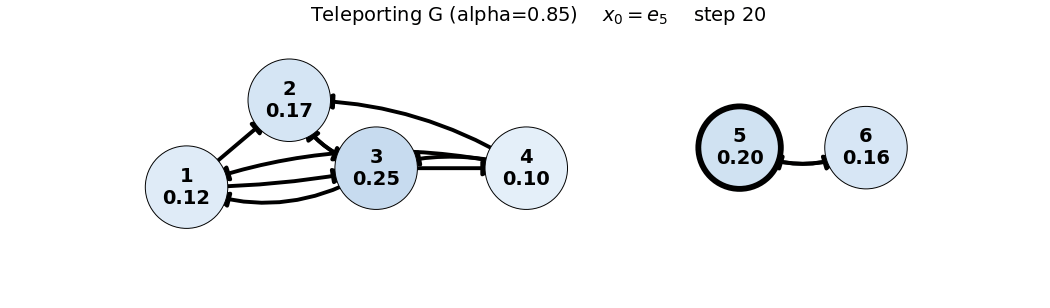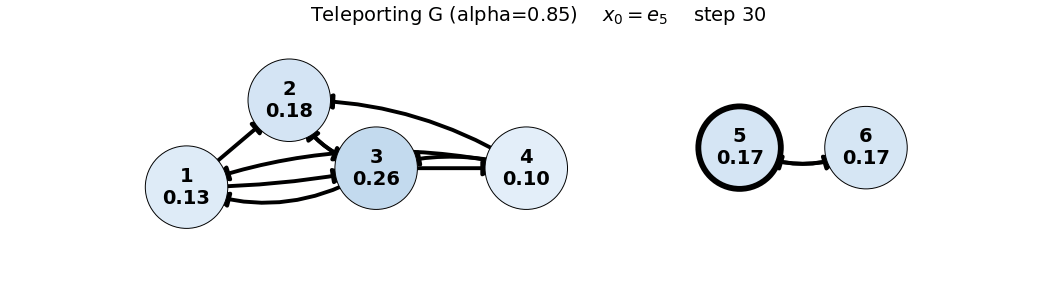
G = 0.85 P + 0.15 \frac{1}{6}\mathbf{1}\mathbf{1}^T = 0.85 P + 0.025 \begin{bmatrix} 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 \end{bmatrix}, \quad x_0 = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 1 \\ 0 \end{bmatrix}

Final States (Teleporting (G))

Final states after 30 iterations for each starting vector:

Uniform: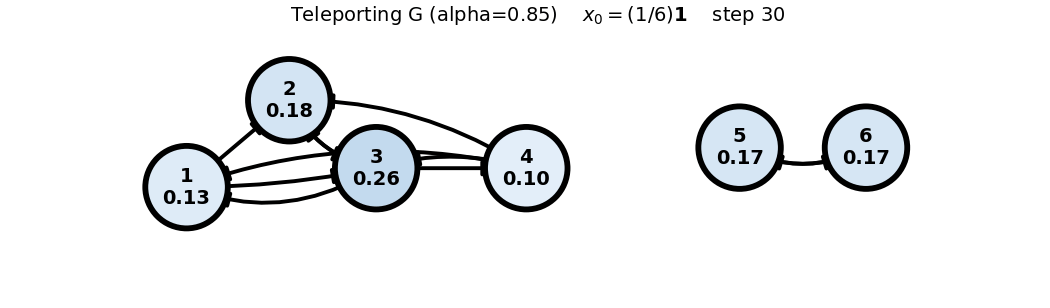

e_1: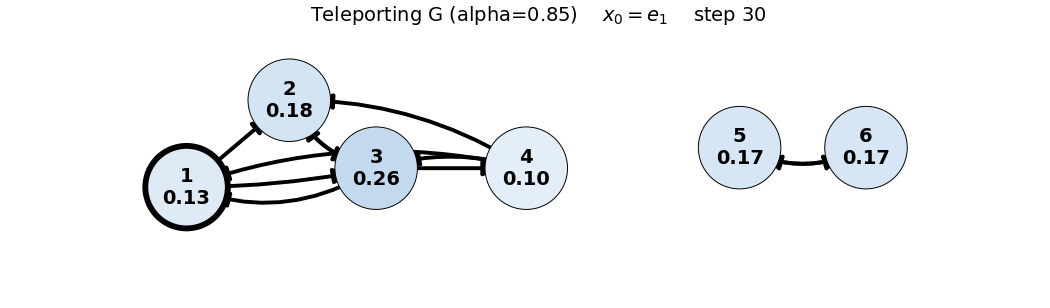

e_4: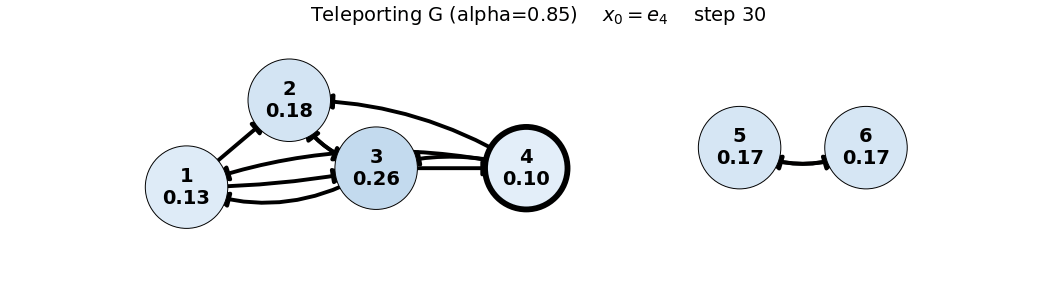

e_5: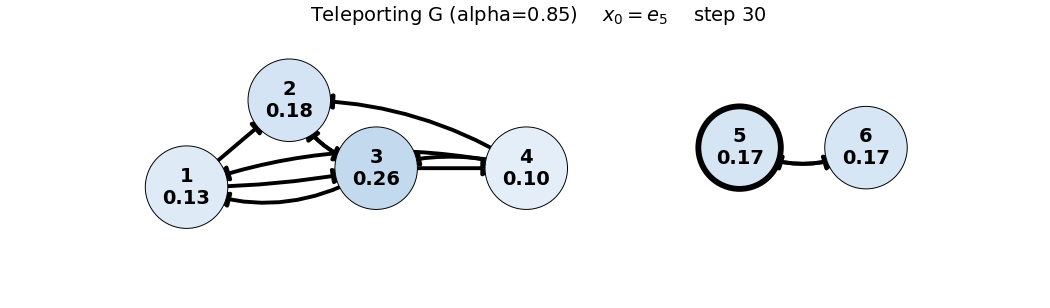

All Final States Comparison

Raw (Q):

Uniform:

e_1:

e_4:

e_5:

Corrected (P):

Uniform:

e_1:

e_4:

e_5:

Teleporting (G):

Uniform:

e_1:

e_4:

e_5: