Ch2 Lecture 3
Difference Equations
Difference Equations
Example: Digital Filters
Digital Filters
Another use for difference equations:
y_{k}=a_{0} x_{k}+a_{1} x_{k-1}+\cdots+a_{m} x_{k-m}, \quad k=m, m+1, m+2, \ldots,
x is a continuous variable – perhaps sound in time domain, or parts of an image in space.
y is some filtered version of x.
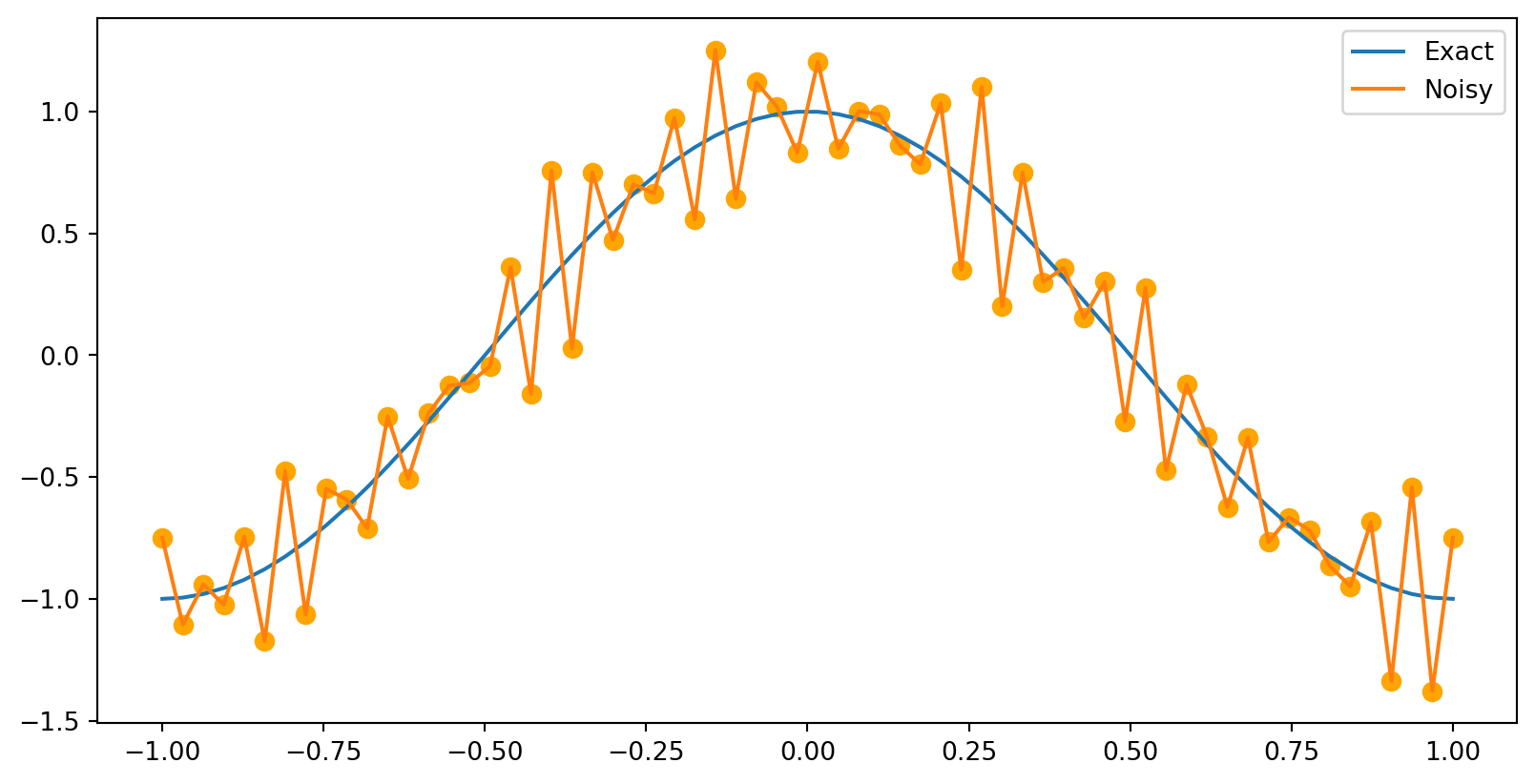
Example: Cleaning up a noisy signal
True signal: f(t)=\cos (\pi t),-1 \leq t \leq 1
Signal plus noise: g(t)=\cos (\pi t)+ \frac{1}{5} \sin (24 \pi t)+\frac{1}{4} \cos (30 \pi t)
Filtered data
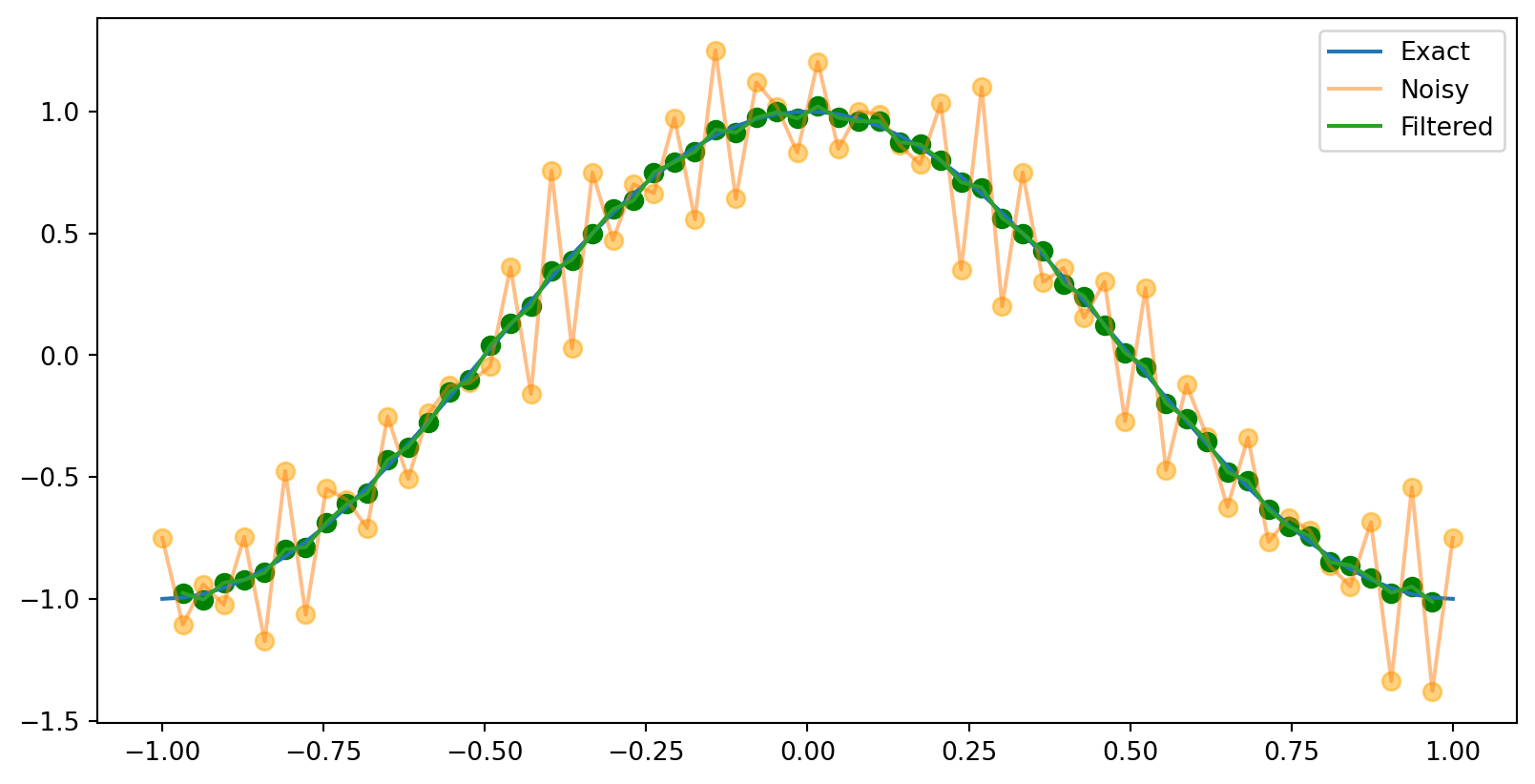
Idea: we can sample nearby points and take a weighted average of them.
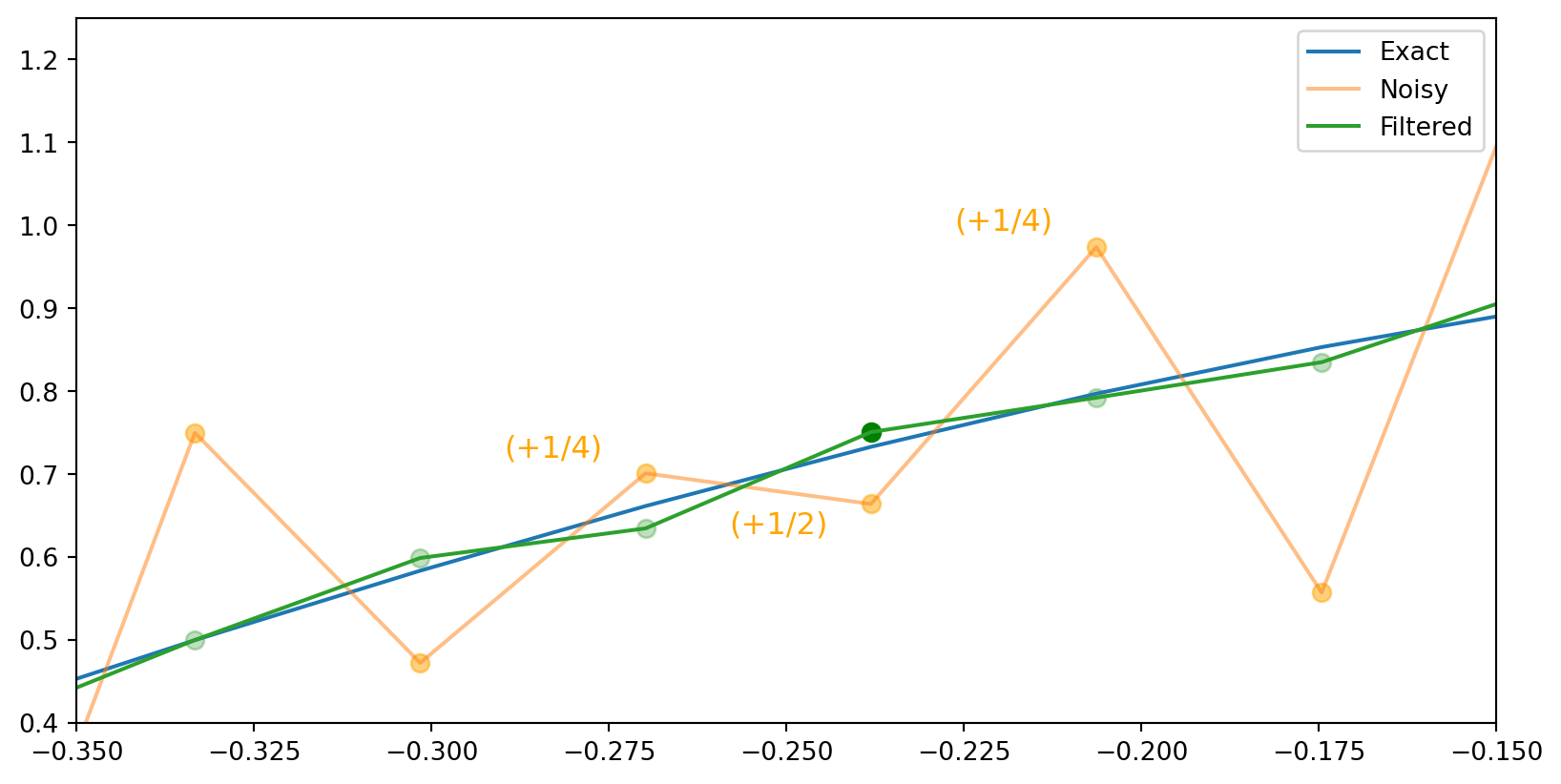
y_{k}=\frac{1}{4} x_{k+1}+\frac{1}{2} x_{k}+\frac{1}{4} x_{k-1}, \quad k=1,2, \ldots, 63
This captured the low-frequency part of the signal, and filtered out the high-frequency noise. That’s just what we wanted! This is called a low-pass filter.
We can zoom in on a few points to see the effect of the filter.
Now you try
See if you can make a figure which will just find the noisyness…
A different filter
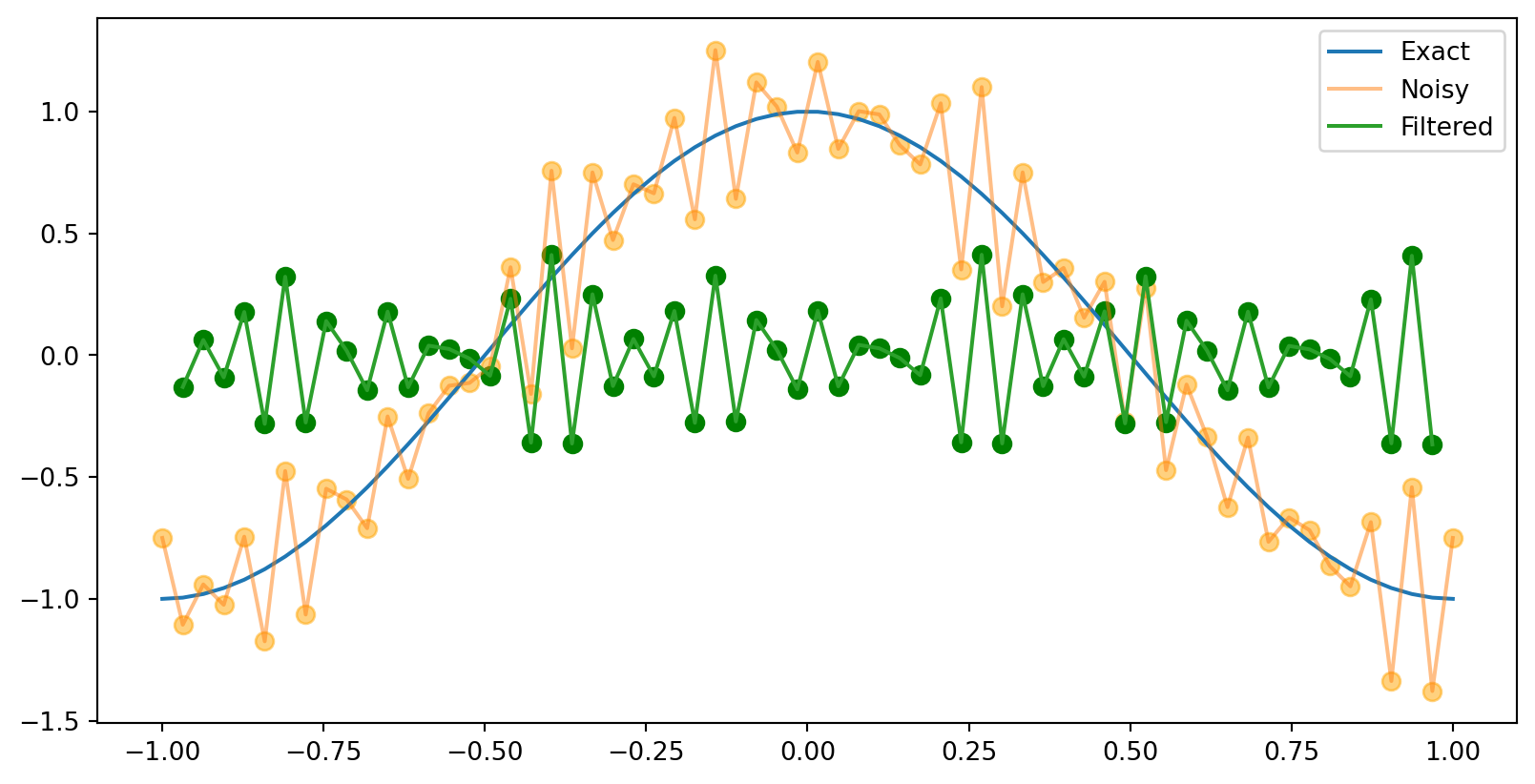
What if we subtract the values at x_{k+1} and x_{k-1} instead of adding them?
y_{k}=-\frac{1}{4} x_{k+1}+\frac{1}{2} x_{k}-\frac{1}{4} x_{k-1}, \quad k=1,2, \ldots, 63
This is a high-pass filter. It captures the high-frequency noise, but filters out the low-frequency signal.
Inverse Matrices
Definition of inverse matrix
Let A be a square matrix.
Inverse for A is a square matrix B of the same size as A
such that A B=I=B A.
If such a B exists, then the matrix A is said to be invertible.
Also called “singular” (non-invertible), or “nonsingular” (invertible)
Conditions for invertibility
Conditions for Invertibility The following are equivalent conditions on the square n \times n matrix A :
The matrix A is invertible.
There is a square matrix B such that B A=I.
The linear system A \mathbf{x}=\mathbf{b} has a unique solution for every right-hand-side vector \mathbf{b}.
The linear system A \mathbf{x}=\mathbf{b} has a unique solution for some right-hand-side vector \mathbf{b}.
The linear system A \mathbf{x}=0 has only the trivial solution.
\operatorname{rank} A=n.
The reduced row echelon form of A is I_{n}.
The matrix A is a product of elementary matrices.
There is a square matrix B such that A B=I.
Elementary matrices
- Each of the operations in row reduction can be represented by a matrix E.
Remember: - E_{i j} : The elementary operation of switching the ith and jth rows of the matrix. - E_{i}(c) : The elementary operation of multiplying the ith row by the nonzero constant c. - E_{i j}(d) : The elementary operation of adding d times the jth row to the ith row.
Find an elementary matrix of size n is by performing the corresponding elementary row operation on the identity matrix I_{n}.
Example: Find the elementary matrix for E_{13}(-4)
Add -4 times the 3rd row of I_{3} to its first row…
E_{13}(-4)=\left[\begin{array}{rrr} 1 & 0 & -4 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right]
Recall an example from the first week:
Solve the simple system
2 x-y=1 \\ 4 x+4 y=20 . \tag{1.5}
\begin{aligned} & {\left[\begin{array}{rrr} 2 & -1 & 1 \\ 4 & 4 & 20 \end{array}\right] \overrightarrow{E_{12}}\left[\begin{array}{rrr} 4 & 4 & 20 \\ 2 & -1 & 1 \end{array}\right] \overrightarrow{E_{1}(1 / 4)}\left[\begin{array}{rrr} 1 & 1 & 5 \\ 2 & -1 & 1 \end{array}\right]} \\ & \overrightarrow{E_{21}(-2)}\left[\begin{array}{rrr} 1 & 1 & 5 \\ 0 & -3 & -9 \end{array}\right] \overrightarrow{E_{2}(-1 / 3)}\left[\begin{array}{lll} 1 & 1 & 5 \\ 0 & 1 & 3 \end{array}\right] \overrightarrow{E_{12}(-1)}\left[\begin{array}{lll} 1 & 0 & 2 \\ 0 & 1 & 3 \end{array}\right] . \end{aligned}
Rewrite this using matrix multiplication: \left[\begin{array}{lll} 1 & 0 & 2 \\ 0 & 1 & 3 \end{array}\right]=E_{12}(-1) E_{2}(-1 / 3) E_{21}(-2) E_{1}(1 / 4) E_{12}\left[\begin{array}{rrr} 2 & -1 & 1 \\ 4 & 4 & 20 \end{array}\right] \text {. }
Remove the last columns in each matrix above. (They were the “augmented” part of the original problem.) All the operations still work:
\left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right]=E_{12}(-1) E_{2}(-1 / 3) E_{21}(-2) E_{1}(1 / 4) E_{12}\left[\begin{array}{rr} 2 & -1 \\ 4 & 4 \end{array}\right] \text {. }
Aha! We now have a formula for the inverse of the original matrix:
A^{-1}=E_{12}(-1) E_{2}(-1 / 3) E_{21}(-2) E_{1}(1 / 4) E_{12}
Superaugmented matrix
- Form the superaugmented matrix [A \mid I].
- If we perform the elementary operation E on the superaugmented matrix, we get the matrix E in the augmented part:
E[A \mid I]=[E A \mid E I]=[E A \mid E]
- This can help us keep track of our operations as we do row reduction
- The augmented part is just the product of the elementary matrices that we have used so far.
- Now continue applying elementary row operations until the part of the matrix originally occupied by A is reduced to the reduced row echelon form of A.
[A \mid I] \overrightarrow{E_{1}, E_{2}, \ldots, E_{k}}[I \mid B]
- B=E_{k} E_{k-1} \cdots E_{1} is the product of the various elementary matrices we used.
Inverse Algorithm
Given an n \times n matrix A, to compute A^{-1} :
Form the superaugmented matrix \widetilde{A}=\left[A \mid I_{n}\right].
Reduce the first n columns of \tilde{A} to reduced row echelon form by performing elementary operations on the matrix \widetilde{A} resulting in the matrix [R \mid B].
If R=I_{n} then set A^{-1}=B; otherwise, A is singular and A^{-1} does not exist.
2x2 matrices
Suppose we have the 2x2 matrix
A=\left[\begin{array}{ll} a & b \\ c & d \end{array}\right]
Do row reduction on the superaugmented matrix:
\left[\begin{array}{ll|ll} a & b & 1 & 0 \\ c & d & 0 & 1 \end{array}\right]
A^{-1}=\frac{1}{D}\left[\begin{array}{rr} d & -b \\ -c & a \end{array}\right]
PageRank revisited
Back to PageRank
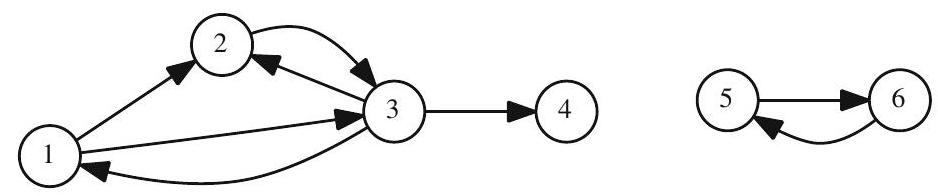
See the animated power iteration (x_{n+1}=Qx_n) on this graph: PageRank animation page.
Do page ranking as in the first week:
- for page j let n_{j} be its total number of outgoing links on that page.
- Then the score for vertex i is the sum of the scores of all vertices j that link to i, divided by the total number of outgoing links on page j. . . . x_{i}=\sum_{x_{j} \in L_{i}} \frac{x_{j}}{n_{j}}
\begin{aligned} & x_{1}=\frac{x_{3}}{3} \\ & x_{2}=\frac{x_{1}}{2}+\frac{x_{3}}{3} \\ & x_{3}=\frac{x_{1}}{2}+\frac{x_{2}}{1} \\ & x_{4}=\frac{x_{3}}{3} \\ & x_{5}=\frac{x_{6}}{1} \\ & x_{6}=\frac{x_{5}}{1} \end{aligned}
PageRank as a matrix equation
Define the matrix Q and vector \mathbf{x} by
Q=\left[\begin{array}{llllll} 0 & 0 & \frac{1}{3} & 0 & 0 & 0 \\ \frac{1}{2} & 0 & \frac{1}{3} & 0 & 0 & 0 \\ \frac{1}{2} & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & \frac{1}{3} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 1 & 0 \end{array}\right], \mathbf{x}=\left(x_{1}, x_{2}, x_{3}, x_{4}, x_{5}\right)
Then the equation x=Q x is equivalent to the system of equations above.
\mathbf{x} is a stationary vector for the transition matrix Q.
Connection between adjacency matrix and transition matrix
- A: adjacency matrix of a graph or digraph
- D: be a diagonal matrix whose i th entry is either:
- the inverse of the sum of all entries in the i th row of \mathrm{A}, or
- zero if if this sum is zero.
- Then Q=A^{T} D is the transition matrix for the page ranking of this graph.
Check.
Remember, for our simple network example, we had the adjacency matrix:
A=\left[\begin{array}{llllll} 0 & 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 1 & 1 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 1 & 0 \end{array}\right]
PageRank as a Markov chain
Think of web surfing as a random process
- each page is a state
- probabilities of moving from one state to another given by a stochastic transition matrix P.
- equal probability of moving to any of the outgoing links of a page
P\stackrel{?}{=}\left[\begin{array}{llllll} 0 & 0 & \frac{1}{3} & 0 & 0 & 0 \\ \frac{1}{2} & 0 & \frac{1}{3} & 0 & 0 & 0 \\ \frac{1}{2} & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & \frac{1}{3} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 1 & 0 \end{array}\right]
Pause: Is P a stochastic matrix?
Correction vector
We can introduce a correction vector, equivalent to adding links from the dangling node to every other node, or to all connecting nodes (via some path).
P=\left[\begin{array}{llllll} 0 & 0 & \frac{1}{3} & \frac{1}{3} & 0 & 0 \\ \frac{1}{2} & 0 & \frac{1}{3} & \frac{1}{3} & 0 & 0 \\ \frac{1}{2} & 1 & 0 & \frac{1}{3} & 0 & 0 \\ 0 & 0 & \frac{1}{3} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 1 & 0 \end{array}\right]
This is now a stochastic matrix “surfing matrix”
Find the new transition matrix Q…
Teleportation
There may not be a single stationary vector for the surfing matrix P.
Solution: Jump around. Every so often, instead of following a link, jump to a random page.
How can we modify the surfing matrix to include this?
Introduce a teleportation matrix E, which is a transition matrix that allows the surfer to jump to any page with equal probability.
Pause: What must E be?
- Let \mathbf{v} be the teleportation vector with entries 1/n -Let \mathbf{e}= (1,1, \ldots, 1) be the vector of all ones.
- Then \mathbf{v e}^{T} is a stochastic matrix whose columns are all equal to \mathbf{v}. This is E.
PageRank Matrix
Let:
- P be a stochastic matrix,
- \mathbf{v} a distribution vector of compatible size
- \alpha a teleportation parameter with 0<\alpha<1.
- Then \alpha P+(1-\alpha) \mathbf{v e}^{T} and
- . . . our goal is to find stationary vectors \left(\alpha P+(1-\alpha) \mathbf{v e}^{T}\right) \mathbf{x}=\mathbf{x} \tag{2.4}
Rearranging,
(I-\alpha P) \mathbf{x}=(1-\alpha) \mathbf{v} \tag{2.5}
Now solve pagerank for our example
Use M.solve(b)…